CMU dlsys 深度学习系统11. 硬件加速 - 知乎 (zhihu.com)

在之前的作业中，实现框架所依赖的底层主要是 numpy 库。本讲开始讨论如何利用硬件进行加速，以及如何利用所学知识编写一个底层库以取代 numpy。学习硬件加速的原因是，现在通常要使用大数据集训练大模型，因此通过这些知识可以了解底层细节，了解代码跑得快或跑得慢的真正影响因素。另外，当有重新实现算子的需求时，也可以知道应该如何根据手头的硬件细节做加速。本讲将对一些通用的硬件加速技巧做介绍

通用的加速技术

通常情况下，机器学习开发框架可以被分为两层，上层为计算图，跟踪计算历史，进行梯度计算。下层为张量线性代数库，允许我们创建具体的多维数组，执行计算。到目前为止，needle 的 NDArray 所依赖的底层线性代数库就是 numpy。然而，机器学习算法会被部署在不同的硬件设备上，例如 CPU、GPU、移动设备或者计算集群，其底层依赖的线性代数库实现也是不一样的，因此有必要对这些库的实现细节有所了解，才能有针对性地进行优化，因此首先来看一些常见的优化技术

第一个常见的技术称为向量化（vectorization）。假设要把两个 256 维向量 A 和 B 相加，结果返回到向量 C 中。最简单的方法是

void vanilla_add(float *A, float *B, float *C) {
    for (int i = 0; i < 256; i++) {
        C[i] = A[i] + B[i];
    }
}

但是在当前常见的设备上，通常有加速单元或加速指令，可以加载内存连续的一部分（称为向量寄存器 vector register），并利用这些寄存器做计算，存储结果。因此，我们可以不从 0 迭代到 256（不含），而是迭代到 64，每个迭代一次从 A 中读入 4 个元素，也从 B 中读入 4 个元素。然后，将读到的这两个向量相加，并将结果通过 store_float4 指令写回到内存中的一个连续区域。整个过程可以通过伪代码描述如下

void vec_add(float *A, float *B, float *C) {
    for (int i = 0; i < 64; ++i) {
        float4 a = load_float4(A + i * 4);
        float4 b = load_float4(B + i * 4);
        float4 c = add_float4(a, b);
        store_float4(C + i * 4, c);
    }
}

这里有一个隐含的要求，就是 A、B 和 C 三个向量的地址需要对齐，三者的起始地址必须是 16 的倍数（1 个浮点数 4 个字节，需要连续 4 个浮点数），所以分配地址时也需要对齐分配。在 64 位机器上如果只是调用普通的 malloc 分配内存，通常起始地址只是 8 的倍数，因此在分配内存时要尤其小心——很多底层线性代数库通常也提供这样的高层对齐内存分配函数

第二个要讨论的是数据布局（data layout）。当我们要存储一个多维矩阵时，至少对于 CPU 内存来说，存储空间实际上是一个扁平的一维数组。因此，对于二维矩阵来说，其每个元素 A[i, j]，可以有两种方法映射到这个一维数组中。以一个 2×3 的矩阵来说，最简单的存储方法是先放第一行，再放第二行——这种方法也称为行主序（row major），映射方法为 A[i, j] => Adata[i * A.shape[1] + j]，例如在这里就是 Adata[i * 3 + j]。这种方法也是人们在常见的编程语言（例如 C 语言）中存储多维数组的方法。不过，在一些古老的编程语言中（例如 FORTRAN），所采取的的是另一种称为列主序（column major）的形式，即先存第一列，再存第二列，以此类推，此时映射方法变为 A[i, j] => Adata[j * A.shape[0] + i]

也可以超越上述两种方法存储数组。一些库引入了“跨步”（stride）的概念，表示偏移量，或者说，在某个轴上放置下一个元素时要累加的增量。假如某个二维数组设置了偏移量属性，那么映射方式变为 A[i, j] => Adata[i * A.strides[0] + j * A.strides[1]]。这种映射方法也可以推广到多轴情况。Stride 是一种比行主序或者列主序更通用的方法。仍以 2×3 的矩阵为例，如果 strides 属性设为 [1, 2]，那么根据上面的映射法则，A[i, j] => Adata[i * 1 + j * 2] = A[i + j * 2] 就是列主序形式，而如果设成 [3,1] 同理可知就对应了行主序形式。另外，stride 使得在对数据做布局变换时更有灵活性，例如

不过，当使用 stride 时，数组的内存地址可能不再连续，使得向量化操作变得比较困难。因此一些线性代数操作先让数组变得“紧凑”，通过类似 PyTorch 中 contiguous 这样的方法让数组占用一块连续空间

第三个技术称为并行化（parallelization）。例如，对于前面的例子，可以加一个注解，利用 openmp 框架进行并行

void vec_add(float *A, float *B, float *C) {
# 下面这一段使用openmp指令进行并行化
# pragma omp parallel for
    for (int i = 0; i < 64; ++i) {
        float4 a = load_float4(A + i * 4);
        float4 b = load_float4(B + i * 4);
        float4 c = add_float4(a, b);
        store_float4(C + i * 4, c);
    }
}

这样，每次迭代时就可以把指令分配到不同的 CPU 上。假设我们有 4 个 CPU 核，则这个循环会进一步划分为 4 块，每一块分给一个 CPU 核

实例研究：矩阵乘法

对矩阵乘法，我们从最直接的算法开始。假设要计算 C = dot(A, B.T)。考虑最简单的情况，三个矩阵都为 n 阶方阵，则有

float A[n][n], B[n][n], C[n][n];

for (int i = 0; i < n; ++i)
    for (int j = 0; j < n; ++j) {
        C[i][j] = 0;
        for (int k = 0; k < n; ++k) {
            C[i][j] += A[i][k] * B[j][k];
        }
    }

这是一个 O(n3) 的算法。尽管矩阵乘法已经有了更快的算法，但是大多数 BLAS 库（Basic Linear Algebra Subprograms，基础线性代数程序集）仍然采用了这种朴素实现——那么这些库为什么会这么快呢？要想理解底层硬件计算逻辑，就需要先了解内存。根据数据存储位置的不同，获取数据的时间也不一样。如果数据放在 DRAM 内存中，大概需要 200 纳秒读取。但是如果数据被预先取到 L1 缓存（更接近 CPU 硬件的存储单元）中，则只需要 0.5 纳秒读取，两者相差了 400 倍。这也是很多高性能计算库要做的事情，就是加速数据的加载

因此，接下来做一些和体系架构相关的分析。假设我们的硬件只有 DRAM 和寄存器，对前面的代码加一些显性注释，指明各个变量存储的位置，有

dram float A[n][n], B[n][n], C[n][n];

for (int i = 0; i < n; ++i)
    for (int j = 0; j < n; ++j) {
        register float c = 0;
        for (int k = 0; k < n; ++k) {
            register float a = A[i][k];
            register float b = B[j][k];
            c += a * b;
        }
        C[i][j] = c;
    }

现在可以计算数据读取次数，有

因此总的读取代价为 2×dram_speed×n3，需要 3 个寄存器

一种加速方法是每次不计算一个元素，而是计算一个子矩阵。将结果矩阵 C 切分为 v1×v2 个区域。对应地，将 A 切分成 v1×v3 个区域，将 B 切分成 v2×v3 个区域，每次都读取一个区域（子矩阵）求内积。这种方法称为寄存器分块矩阵乘法（register tiled matrix multiplication）

dram float A[n/v1][n/v3][v1][v3];
dram float B[n/v2][n/v3][v2][v3];
dram float C[n/v1][n/v2][v1][v2];

for (int i = 0; i < n/v1; ++i) {
    for (int j = 0; j < n/v2; ++j) {
        register float c[v1][v2] = 0;
        for (int k = 0; k < n/v3; ++k) {
            register float a[v1][v3] = A[i][k];
            register float b[v2][v3] = B[j][k];
            c += dot(a, b.T);
        }
        C[i][j] = c;
    }
}

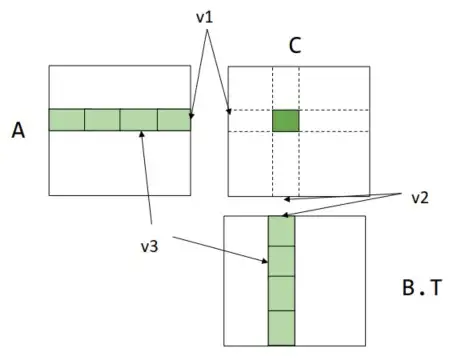
对上述代码进行分析

这意味着总的读取代价不再是固定的�3，而是由�1 和�2（称为分块因子 tiling factor）决定。最优的做法肯定是尽量放大�1 和�2，但是也要注意不要超过寄存器的数量（注意�3 不影响读取次数，所以可以设为 1）

可以再往深想一下：为什么这种方法可以减少数据加载次数呢？因为最内层的数据会被复用很多次，a 中的数据会被复用�2 次，因此开销的降低实际来源于我们把变量读入寄存器以后复用了内存

接下来考虑另一种更加复杂的情况，称为行缓存（cache line）

dram float A[n/b1][b1][n];
dram float B[n/b2][b2][n];
dram float C[n/b1][n/b2][b1][b2];

for (int i = 0; i < n/b1; ++i) {
    l1cache float a[b1][n] = A[i];
    for (int j = 0; j < n/b2; ++j) {
        l1cache b[b2][n] = B[j];
        C[i][j] = dot(a, b.T);
    }
}

这里引入了两个分块因子�1 和�2，期望每次能计算得到�1×�2 大小的子矩阵。这里不是将数据读入寄存器，而是每次将若干行数据读入 L1 缓存（通常不能直接操作 L1 缓存，这里仅做示意用）。对上述代码做分析

进一步地，我们希望�1 和�2 是�1 和�2 的整数倍，这样可以进一步再利用寄存器分块策略。另外，�1×�+�2×�也不应超出 L1 缓存的大小。将上述两部分代码整合在一起，有

dram float A[n/b1][b1/v1][n][v1];
dram float B[n/b2][b2/v2][n][v2];

for (int i = 0; i < n/b1; ++i) {
    l1cache float a[b1/v1][n][v1] = A[i];
    for (int j = 0; j < n/b2; ++j) {
        l1cache float b[b2/v2][n][v2] = B[j];
        for (int x = 0; x < b1/v1; ++x) {
            for (int y = 0; y < b2/v2; ++y) {
                register float c[v1][v2] = 0;
                for (int k = 0; k < n; ++k) {
                    register float ar[v1] = a[x][k][:];
                    register float br[v2] = b[y][k][:];
                    C += dot(ar, br.T);
                }
            }
        }
    }
}

这段代码最内层 ar 的加载次数为�/�1×�/�2×�1/�1×�2/�2×�×�1=�3/�2，类似的，br 的加载次数为�3/�1。这两个变量都是从 L1 缓存加载而来。将数据从内存读入 L1 缓存的次数，由上面的计算，为�2 和�3/�1

尽管这只是在一个理想模型上做的近似推导，且最后的读取次数仍然是�3 量级，但是由于各个分块因子的存在，代码的耗时比原先切实的�3 次读取时间快很多，而如果进一步优化和重组代码，应该还有提升空间（例如加入并行化）

再次强调，速度的提升来自于变量的复用。在寄存器分块的例子中，a 被复用了�2 次，b 被复用了�1 次，因此真正要做的是思考复用的模式。观察代码中循环的模式

C[i][j] = sum(A[i][k] * B[j][k], axis=k)

A 中元素的轴独立于 j，所以如果将 j 分为 v 块，就复用了 v 次 A（迭代过程缺哪个，就分哪个，例如 B 的迭代缺少 i，则将 i 分 v 块就是复用了 v 次 B）。